基于QHA计算各向异性的热膨胀系数
目前基于QHA的各向异性热膨胀计算方法有三种,第一种是QHA拟合法,第二种是轴格林艾森法,第三种则是ZSISA及其变体。
这三种算法各有特色,这里汇总介绍一下。
轴格林艾森法
这个方法一般适用于立方,四方和正交体系(晶胞自由度≤3且不涉及角度)。
尽管低对称性晶体也应有相应算法可以求出热膨胀张量,但至少我目前尚未发现现成的脚本或者程序支持计算,需要一定的物理和编程基础。
不推荐材料人对以上三种晶体外的体系使用轴格林艾森法。
Important
在高温区,轴格林艾森法会有饱和现象,预测的热膨胀系数会逐渐趋于定值。
理论部分
格林艾森参数的定义如下:
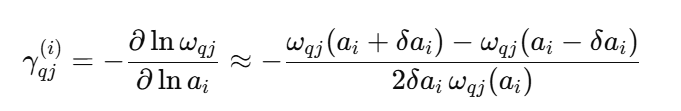
可以看到,格林艾森参数,是描述微小应变引起的声子频率变化关系的参数。
所谓轴格林艾森参数,即是应变沿着轴时,计算声子得到的格林艾森参数,在计算上与普通的格林艾森参数并无区别。
但是轴格林艾森参数可以通过一个公式,和轴热膨胀系数联系起来,如下:
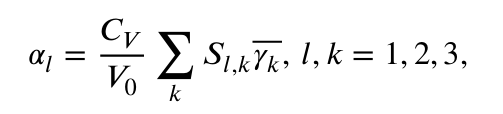
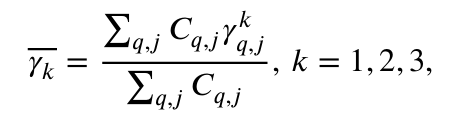
公式里符号的含义可以在 这篇文献 中找到。
可以看出,想要计算一个轴热膨胀系数,需要以下数据:
- 平衡体积、平衡体积下的声子谱(以便求解模式热容、模式格林艾森参数)
- 一拉伸一压缩的声子谱(以便求解模式格林艾森参数)
- 弹性系数或者柔度矩阵
这里有个非常有意思的变换,就是宏观格林艾森参数的定义,宏观格林艾森参数 x 宏观热容 = (模式热容 x 模式格林艾森参数)的求和
代码实现
代码源自 Github 的无名客,我进行了翻新,让它可以使用python3来运行。
import numpy as np
from numpy import linalg as LA
import yaml
# -----------------------------
# 读取 grun_tec.in 文件
# -----------------------------
with open('grun_tec.in', 'r') as f:
lines = [line.strip() for line in f.readlines()]
# 解析参数
An = lines[0].split('=')[1].split(',')[0].strip() # 'y' 或 'n'
Dm = float(lines[1].split('=')[1].split(',')[0].strip()) # 维度 2/3
IL = int(lines[2].split('=')[1].split(',')[0].strip()) # 独立晶格常数数量 1/2/3
B = int(lines[3].split('=')[1].split(',')[0].strip()) # 声子支数
dd = float(lines[4].split('=')[1].split(',')[0].strip()) # Strain
bi = float(lines[5].split('=')[1].split(',')[0].strip()) # 未使用
fn0 = lines[6].split('=')[1].split(',')[0].strip()
fn1 = lines[7].split('=')[1].split(',')[0].strip()
fn2 = lines[8].split('=')[1].split(',')[0].strip()
fn3 = lines[9].split('=')[1].split(',')[0].strip()
fn4 = lines[10].split('=')[1].split(',')[0].strip()
fn5 = lines[11].split('=')[1].split(',')[0].strip()
fn6 = lines[12].split('=')[1].split(',')[0].strip()
c11 = float(lines[13].split('=')[1].split(',')[0].strip())
c22 = float(lines[14].split('=')[1].split(',')[0].strip())
c33 = float(lines[15].split('=')[1].split(',')[0].strip())
c12 = float(lines[16].split('=')[1].split(',')[0].strip())
c13 = float(lines[17].split('=')[1].split(',')[0].strip())
c23 = float(lines[18].split('=')[1].split(',')[0].strip())
Tm = int(lines[19].split('=')[1].split(',')[0].strip())
v0 = float(lines[20].split('=')[1].split(',')[0].strip()) * 1e-30 # m^3
# -----------------------------
# 常量
# -----------------------------
pi = np.pi
kb = 1.381e-23 # J/K
hb = 1.055e-34 # J*s
# -----------------------------
# 计算宏观格林艾森参数和比热
# -----------------------------
def macrogrun(f0, f1, f2, w, dd, T, jm):
"""
f0: 平衡频率 rad/s
f1: 拉伸频率 rad/s
f2: 压缩频率 rad/s
w: 声子权重
dd: Strain
T: 温度
jm: 声子支数
"""
mode_g = -1/f0 * (f2 - f1) / (2*dd) # 模格林艾森参数
c1 = hb * f0 / (kb * T)
c2 = np.exp(-c1)
cv = w * kb * c1**2 * c2 / (1 + c2**2 - 2*c2)
Cv = cv.sum() / w.sum() * jm
I = cv * mode_g
MG = I.sum() / cv.sum()
return MG, Cv
# -----------------------------
# 解析 phonopy mesh.yaml 文件
# -----------------------------
def extract_mesh_yaml(fn, num_branches):
"""
从 phonopy mesh.yaml 提取 mode_index, weight, frequency
支持新旧 phonopy YAML 格式
输出 numpy 数组 shape=(num_modes, 3) -> [mode_index, weight, frequency(THz)]
"""
with open(fn, 'r') as f:
data = yaml.safe_load(f)
if "phonon" not in data:
raise ValueError(f"No 'phonon' section found in {fn}")
result = []
for qpoint in data["phonon"]:
weight = qpoint.get("weight", 1)
bands = qpoint.get("band", [])
# 兼容旧 phonopy YAML
if bands and isinstance(bands[0], dict) and "frequency" not in bands[0] and "frequencies" in bands[0]:
# 旧格式 frequencies 列表
freqs = bands[0]["frequencies"]
for idx, f in enumerate(freqs, start=1):
result.append([idx, weight, f])
else:
for idx, band in enumerate(bands, start=1):
freq = band.get("frequency", 0.0)
result.append([idx, weight, freq])
return np.array(result)
# -----------------------------
# 提取频率数据
# -----------------------------
t0 = extract_mesh_yaml(fn0, B)
t1 = extract_mesh_yaml(fn1, B)
t2 = extract_mesh_yaml(fn2, B)
f0 = t0[:,2] * 1e12 * 2 * pi
f1 = t1[:,2] * 1e12 * 2 * pi
f2 = t2[:,2] * 1e12 * 2 * pi
w = t0[:,1]
Tem = np.arange(1, Tm) # 温度数组
X = len(Tem)
# -----------------------------
# 初始化输出矩阵
# -----------------------------
tec = None
MG_arr = None
# -----------------------------
# 各向同性或各向异性计算逻辑
# -----------------------------
if An == 'n':
# 各向同性
tec = np.zeros((1,X))
MG_arr = np.ones((1,X))
if Dm == 2:
ec = np.array([[c11,c12],[c12,c11]])*1e9
sc = LA.inv(ec)
for i,T in enumerate(Tem):
mg, cv = macrogrun(f0,f1,f2,w,dd,T,B)
mg /= Dm
MG_arr[0,i] = mg
tec[0,i] = mg*(sc[0,0]+sc[0,1])*cv/v0
else:
ec = np.array([[c11,c12,c12],[c12,c11,c12],[c12,c12,c11]])*1e9
sc = LA.inv(ec)
for i,T in enumerate(Tem):
mg, cv = macrogrun(f0,f1,f2,w,dd,T,B)
mg /= Dm
MG_arr[0,i] = mg
tec[0,i] = mg*(sc[0,0]+sc[0,1]+sc[0,2])*cv/v0
else:
# 各向异性
t3 = extract_mesh_yaml(fn3, B)
t4 = extract_mesh_yaml(fn4, B)
f3 = t3[:,2]*1e12*2*pi
f4 = t4[:,2]*1e12*2*pi
MG_arr = np.ones((IL,X))
tec = np.zeros((IL,X))
# 如果 IL==3,需要 fn5, fn6
if IL == 3:
t5 = extract_mesh_yaml(fn5, B)
t6 = extract_mesh_yaml(fn6, B)
f5 = t5[:,2]*1e12*2*pi
f6 = t6[:,2]*1e12*2*pi
print("3D anisotropic material with 3 independent lattice constants")
else:
print("3D anisotropic material with 2 independent lattice constants (e.g. tetragonal)")
# 构建弹性常数矩阵
ec = np.array([[c11,c12,c13],[c12,c22,c23],[c13,c23,c33]])*1e9
sc = LA.inv(ec)
for i,T in enumerate(Tem):
mg0, cv = macrogrun(f0,f1,f2,w,dd,T,B)
mg1, cv = macrogrun(f0,f3,f4,w,dd,T,B)
if IL==3:
mg2, cv = macrogrun(f0,f5,f6,w,dd,T,B)
MG_arr[0,i] = mg0
MG_arr[1,i] = mg1
MG_arr[2,i] = mg2
tec[0,i] = (mg0*sc[0,0] + mg1*sc[0,1] + mg2*sc[0,2]) * cv/v0
tec[1,i] = (mg0*sc[1,0] + mg1*sc[1,1] + mg2*sc[1,2]) * cv/v0
tec[2,i] = (mg0*sc[2,0] + mg1*sc[2,1] + mg2*sc[2,2]) * cv/v0
else: # IL==2
mg0 /= 2
MG_arr[0,i] = mg0
MG_arr[1,i] = mg1
tec[0,i] = (mg0*sc[0,0] + mg0*sc[0,1] + mg1*sc[0,2]) * cv/v0
tec[1,i] = (mg0*sc[2,0] + mg0*sc[2,1] + mg1*sc[2,2]) * cv/v0
# -----------------------------
# 输出 LTEC.dat
# -----------------------------
ltec = np.vstack((Tem, MG_arr, tec)).T
Y = ltec.shape[1]
with open('LTEC.dat', 'w') as fd:
fd.write(f"{'T (K)':<6}")
YY = (Y-1)//2
for _ in range(YY):
fd.write(f"{'Macro Gruneisen':^25}")
for _ in range(YY):
fd.write(f"{'LTEC (K-1)':^25}")
fd.write('\n')
for row in ltec:
fd.write(f"{int(row[0]):<6}")
fd.write(f"{row[1]: 20.15e}")
for val in row[2:]:
fd.write(f"{val: 25.15e}")
fd.write('\n')
print("----------- Successful! ------------")
需要一个准备文件,grun_tec.in
声子的计算由phonopy完成。
如下,
An=y, !Anisotropic (y) or not (n)
Dim=3, !2(D) or 3(D)
Independ=2, !Independent lattice constants
B=12, !Branches of phonons
Delta=0.01, !Strain
#strain=1, !This parameter is not of use now. (^.^)
fname0=mesh0.yaml, !Phonon filenames, 0 is for the equilibrium volume
fname1=mesh1.yaml, !1-6 are phonon filenames under strains. 1 and 2 are compressed and stretched, along the same direction.
fname2=mesh2.yaml,
fname3=mesh3.yaml,
fname4=mesh4.yaml,
fname5=t5.dat,
fname6=t6.dat,
C11=1090.12069, !Elastic constants, in GPa.
C22=1090.11933,
C33=47.17890,
C12=20.186738,
C13=-12.47374,
C23=-12.47373,
Tmax=800, !Maximum temperature, in K
v0=33.57, !Equilibrium volume, in A^3
小结
对声子积分有了深入的认识。
所谓波矢q和支数j,就是mesh.yaml中的q-point和band。
从头加到尾,也就是对声子在布里渊区内积分的近似。
计算模式热容时,注意把phonopy中的频率转化成角频率。