用于搭建神经网络的函数

🗓️ 2025-05-19 🗂️ 深度学习

用于搭建神经网络的函数

前言

此处记录常见的神经网络函数，排名不分先后。

全连接层

1. nn.Linear()

对输入数据施加一个仿射线性变换，一般使用指定两个参数，是输入矩阵和输出矩阵的最高维的size。（因为最高维一般是特征维度，这个函数就是用来控制特征维度size大小的）

这里是CGCNN的图卷积操作公式，这里的W（权重），b（偏置）其实全连接层决定的。看到这样的写法就要明白其实是经历了一个全连接层。

total_gated_fea = self.fc_full(total_nbr_fea)
        
total_gated_fea = self.bn1(total_gated_fea.view(
	-1, self.atom_fea_len*2)).view(N, M, self.atom_fea_len*2)
nbr_filter, nbr_core = total_gated_fea.chunk(2, dim=2)
nbr_filter = self.sigmoid(nbr_filter)
nbr_core = self.softplus1(nbr_core)

对应代码就是进过全连接层后，（再进行批标准化，chunk分割，这些公式里没有体现），然后施加$\sigma$函数和激活函数（g）。

激活函数

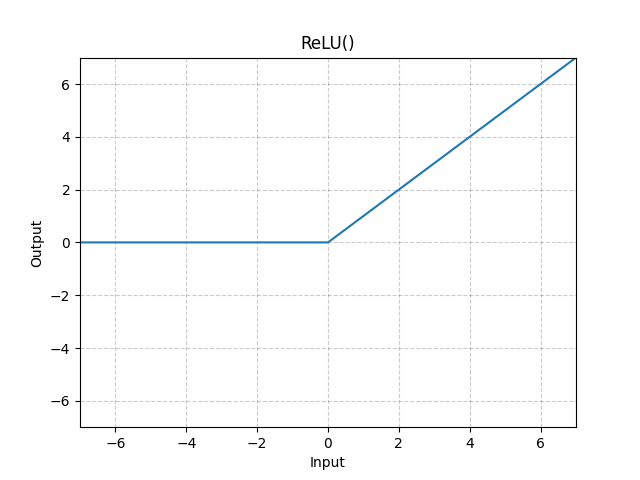
1. nn.ReLU()

这个激活函数不用指定输入输出特征的维度，它只是把所有特征变为非负，对于正值保留原始值，对于负值则转化为0。

2. nn.Softmax()

对一个n维的张量施加Softmax()函数，使得其沿某个维度的元素值的和为1。所以接受一个dim参数来指定维度。

$$ \mathrm{Softmax}(x_i)=\frac{\mathrm{exp}(x_i)}{\sum_{j}\mathrm{exp}(x_j)} $$

这里简单插入一下Pytorch中有关dim的实践。

比如说一个张量的size是(4,2,3)，那么他的dim=0指的是4，dim=1指的是2，dim=2指的是3。

比如说对于这个张量，我有个和Pytorch相反的习惯，我习惯先看每行有多少个元素，是3。我就误以为它的dim=0对应的是3。

其实不然，深度学习中，dim最大值对应维度的size，往往对应样本的特征数。

一个简单的二维的深度学习的输入张量的size一般是这样的：(batch_size,features)。

tensor([[[0.3299, 0.4336, 0.2365],
         [0.0695, 0.0668, 0.8638]],

        [[0.8114, 0.1116, 0.0770],
         [0.3142, 0.1086, 0.5772]],

        [[0.3178, 0.4508, 0.2315],
         [0.1620, 0.2610, 0.5770]],

        [[0.4454, 0.4082, 0.1464],
         [0.2974, 0.5297, 0.1729]]])

3. nn.LogSoftmax()

对一个n维的张量施加log(Softmax())函数，通常用于获取对数概率，并与损失函数nn.NLLLoss()一起使用

4. nn.Softmax2d()

针对3维(C,H,W)或4维(N,C,H,W)的输入，它总是沿着C对应的维度对张量施加Softmax()函数

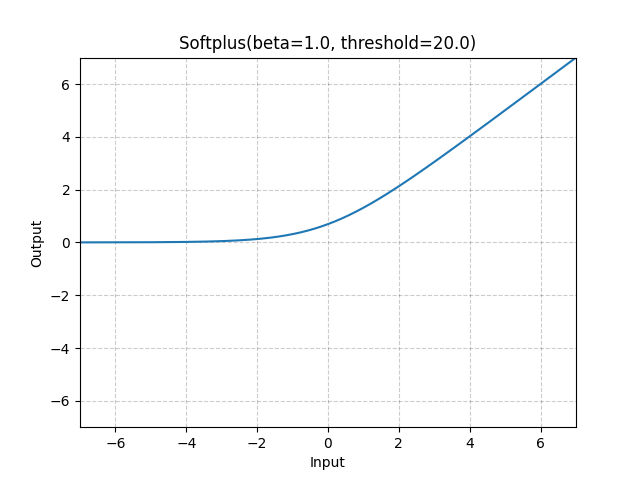
5. nn.Softplus()

对每个张量元素施加 Softplus 函数。这是一个ReLU函数的光滑近似，用于保证正的输出。

默认$\beta$值为1，当输入值*$\beta$大于一定门槛（默认值20）时，会变成线性。

$\mathrm{Softplus}(x)=\frac{1}{\beta}*\log(1+\exp(\beta * x))$

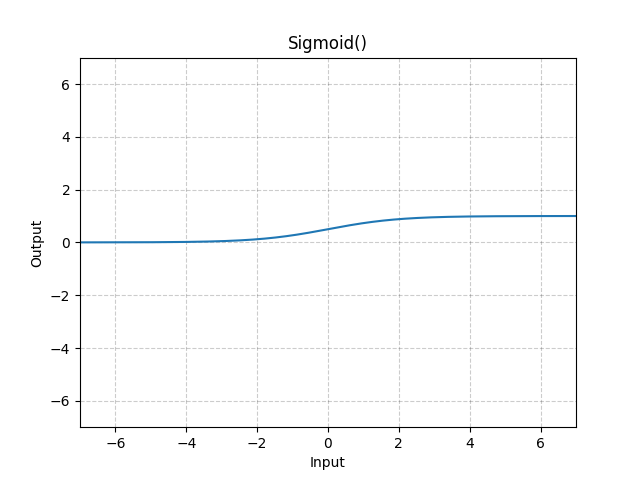
6. nn.Sigmoid()

对张量的每个元素施加Sigmoid函数。对于小于0的输入，输出0-0.5；对于大于0的输入，输出0.5-1。整体是非负的。

$\mathrm{Sigmoid}(x)=\sigma(x)=\frac{1}{1+\exp(-x)}$

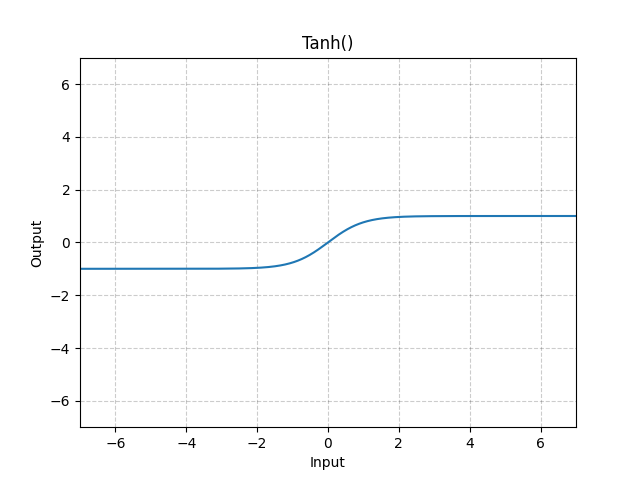
7. nn.Tanh

对张量的每个元素施加双曲正切函数，输出值范围为(-1,1)。

$\mathrm{Tanh}(x)=\mathrm{tanh}(x)=\frac{\exp(x)-\exp(-x)}{\exp(x)+\exp(-x)}$

批标准化

1. nn.BatchNorm1d()

对二维(N,C)或三维(N,C,L)的输入进行批标准化。

对于二维输入，其实N是batch大小，C是特征数，这里叫Channels，是沿着列求平均和方差的。并且这个函数求的是有偏方差。

对于三维输入，可以理解成先转化为(N*L,C)，再用二维的处理方法得到结果，再展开。

正则化

参考文献

在深度学习中，正则化通常用于约束模型的复杂度、防止过拟合、提高模型的泛化能力和鲁棒性。

1. nn.Dropout()

在每次前向传播时，以一定概率让张量中的某些元素归零。防止过拟合。常用于分类任务。不要用于回归任务。

接受一个浮点数，用于表示概率，默认值是0.5。

2. L1正则化

L1正则化、也称Lasso正则化。就是在损失函数中引入一个与模型权重的L1范数相关的值，作为惩罚项，用于控制（限制）模型的复杂度和防止过拟合。

$L_{L1}=L_{data}+\lambda\begin{matrix} \sum_{i=1}^n |w_i| \end{matrix}$

3. L2正则化

L2正则化，也称Ridge正则化、权重衰减。与L1正则化类似，就是在损失函数中引入一个与模型权重的L2范数相关的值，作为惩罚项，用于控制（限制）模型的复杂度和防止过拟合。它鼓励模型用小的模型参数。

$L_{L1}=L_{data}+\lambda||w||_2^2$

这里，

$$ ||w|| _2 ^2 = \sum_{i=1}^n w_i^2 $$

4. Elastic Net 正则化

采用L1正则化和L2正则化的组合。

5. 早停止和数据增强

早停止：即检测模型在验证集上的性能，当模型在验证集的性能出现下降时停止训练，避免过拟合。

数据增强：对数据进行一定变换来增强数据的多样性。如在图像分类时，对图片进行旋转、剪裁、翻转等操作。

Comment